Question

Sketch f(x) = 5x2 - 20 labelling any intercepts.​

Answer 1

• The graph of the function is attached below.

• The x-intercepts will be: (2, 0), (-2, 0)

• The y-intercept will be: (-20, 0)

Step-by-step explanation:

Given the function

`f\left(x\right)\:=\:5x^2-\:20`

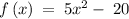
As we know that the x-intercept(s) can be obtained by setting the value y=0

so

`y=\:5x^2-\:20`

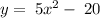
switching sides

`5x^2-20=0`

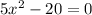
Add 20 to both sides

`5x^2-20+20=0+20`

`5x^2=20`

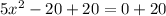
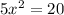
Dividing both sides by 5

`(5x^2)/(5)=(20)/(5)`

`x^2=4`

`\mathrm{For\:}x^2=f\left(a\right)\mathrm{\:the\:solutions\:are\:}x=√(f\left(a\right)),\:\:-√(f\left(a\right))`

`x=√(4),\:x=-√(4)`

`x=2,\:x=-2`

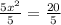
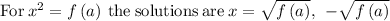
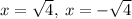
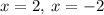
so the x-intercepts will be: (2, 0), (-2, 0)

we also know that the y-intercept(s) can obtained by setting the value x=0

so

`y=\:5(0)^2-\:20`

`y=0-20`

`y=-20`

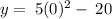
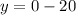
so the y-intercept will be: (-20, 0)

From the attached figure, all the intercepts are labeled.