Question

Question

2. Determine
the
acute
angle
between the planes
x - 2y + 5z = 3
2x + y - 3z = 15.
Distance of a plane from the origin:​

Answer 1

Acute angle between the two planes: approximately
`43^\circ`.

Explanation:

Find the normal vector of each plane:

• The normal vector of the plane
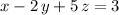  `x - 2\, y + 5\, z = 3` is
  `\displaystyle \begin{bmatrix}1 \\ -2 \\ 5\end{bmatrix}`.
• The normal vector of the plane
  `2\, x + y - 3\, z = 15` is
  `\displaystyle \begin{bmatrix}2 \\ 1\\ -3\end{bmatrix}`.

As the name suggests, there is a
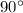`90^\circ` angle between a plane and its normal vector. The following four angles will correspond to the vertices of a quadrilateral:

• The
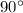  `90^\circ` angle between the first plane and its normal vector.
• The angle between the normal vector of each plane.
• The
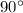  `90^\circ` angle between the second plane and its normal vector.
• The smallest angle between these two planes.

The sum of these four angles should be
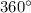`360^\circ`. Two of these four angles were known to be
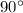`90^\circ`. Once the third angle (the angle between the two normal vectors) is found, subtractions would give the measure of the other angle (the smallest angle between these two planes.)

Make use of the dot product to find the angle between these two normal vectors. Let
`\theta` denote the angle between these two vectors.

`\displaystyle \cos \theta = \frac{\begin{bmatrix}1 \\ -2 \\ 5\end{bmatrix} \cdot \begin{bmatrix}2 \\ 1 \\ -3\end{bmatrix}}{√(1^2 + (-2)^2 + 5^2) \cdot √(2^2 + 1^2 + (-3)^2)} \approx -0.73193`.

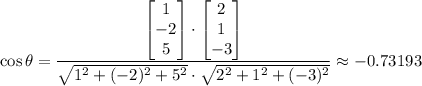Before continuing, notice that the smallest angle between the two planes would be
`360^\circ - 90^\circ - 90^\circ - \theta = 180^\circ - \theta`.

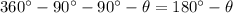Consider the identity:
`\cos\left(180^\circ - \theta\right) = -\cos \theta`.

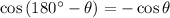In other words,
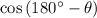`\cos\left(180^\circ - \theta\right)`, the cosine of the smallest angle between the two planes (which the question is asking for) will be the opposite of
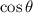`\cos \theta`, the cosine of the angle between the two normal vectors.

Therefore, the cosine of the smallest angle between the two planes will be
`-(-0.73193) = 0.73193`.

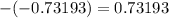Apply the inverse cosine function to find the size of that angle:

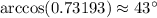`\arccos(0.73193) \approx 43^\circ`.