Question

L1 and L2 are two straight lines. The origin of the coordinate axes is O. L1 has equation 5x + 10y = 8 L2 is perpendicular to L1 and passes through the point with coordinates (8, 6) L2 crosses the x-axis at the point A. L2 intersects the straight line with equation x = –3 at the point B. Find the area of triangle AOB. Show your working clearly.

Answer 1

40 sq units

Explanation:

`5x + 10y = 8\\\Rightarrow y=(8-5x)/(10)\\\Rightarrow y=-(1)/(2)x+(2)/(5)`

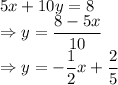
Slope of
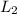`L_2` is
`m_2`

`m_1m_2=-1\\\Rightarrow m_2=-(1)/(m_1)\\\Rightarrow m_2=-(1)/(-(1)/(2))\\\Rightarrow m_2=2`

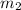
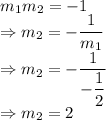
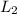`L_2` passes through point
`(8,6)`

`y-6=2(x-8)\\\Rightarrow y=2x-16+6\\\Rightarrow y=2x-10`

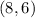
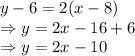
Point at x axis where
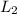`L_2` intersects is

`0=2x-10\\\Rightarrow x=(10)/(2)\\\Rightarrow x=5`

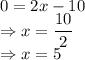
Point
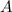`A` of the triangle will be
`(5,0)`

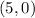
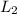`L_2` intersects line
`x=-3`. The point is

`y=2*(-3)-10\\\Rightarrow y=-6-10\\\Rightarrow y=-16`

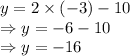
The points of the triangle are
`A(5,0), O(0,0), B(-3,-16)`

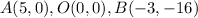
Area of triangle is given by

`A=(|A_x(B_y-O_y)+B_x(A_y-O_y)+O_x(A_y-B_y)|)/(2)\\\Rightarrow A=(|5(-16-0)+-3(0-0)+0(0-(-16))|)/(2)\\\Rightarrow A=40\ \text{sq units}`

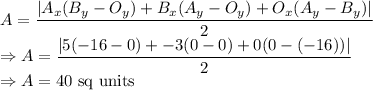
The area of the triangle is 40 sq units.