Question

At what angle does a diffraction grating produce a second-order maximum for light having a first-order maximum at 20.0 degrees?

Answer 1

At 43.2°.

Explanation:

To find the angle we need to use the following equation:

`d*sin(\theta) = m\lambda`

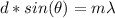
Where:

d: is the separation of the grating

m: is the order of the maximum

λ: is the wavelength

θ: is the angle

At the first-order maximum (m=1) at 20.0 degrees we have:

`(\lambda)/(d) = (sin(\theta))/(m) = (sin(20.0))/(1) = 0.342`

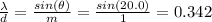
Now, to produce a second-order maximum (m=2) the angle must be:

`sin(\theta) = (\lambda)/(d)*m`

`\theta = arcsin((\lambda)/(d)*m) = arcsin(0.342*2) = 43.2 ^(\circ)`

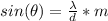
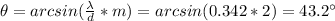
Therefore, the diffraction grating will produce a second-order maximum for the light at 43.2°.

I hope it helps you!