Answer:
2.12 seconds
Explanation:
Given
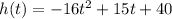
Required
Determine how long the ball hits the ground
When the ball hits the ground means that

So, we have that:
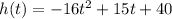 becomes
becomes
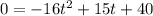
Reorder
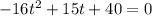
Multiply through by -1
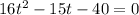
Solve using quadratic:

Where
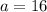

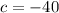
So, we have:
 becomes
becomes
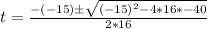
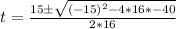
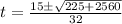

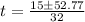
Split:
 or
or
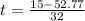
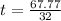 or
or
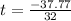
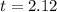 or
or
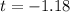
But time can't be negative
So:
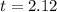
Hence, time to hit the ground is 2.12 seconds