Answer:
The line presented has an undefined slope.
Explanation:
We are given two points of a line: (-1, 1) and (-1, 4).
Coordinate pairs in mathematics are labeled as (x₁, y₁) and (x₂, y₂).
- The x-coordinate is the point at which if a straight, vertical line were drawn from the x-axis, it would meet that line.
- The y-coordinate is the point at which if a straight, horizontal line were drawn from the y-axis, it would meet that line.
Therefore, we know that the first coordinate pair can be labeled as (x₁, y₁), so, we can assign these variables these "names" as shown below:
We also can use the same naming system to assign these values to the second coordinate pair, (-1, 4):
We also need to note the rules about slope. There are different instances in which a slope can either be defined or it cannot be defined.
Circumstance 1: As long as the slope is not equal to zero, there can be a
- positive slope,

- negative slope,
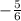
Circumstance 2: If the slope is completely vertical (there is not a "run" associated with the line), there is an undefined slope. This is the slope of a vertical line. An example would be a vertical line (the slope is still zero).
Circumstance 3: If the line is a horizontal line (the line does not "rise" at all), then the slope of the line is zero.
Therefore, a slope can be positive, negative, zero, or undefined.
Now, we need to solve for the line we are given.
The slope of a line is determined from the slope-intercept form of an equation, which is represented as
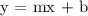 .
.
The slope is equivalent to the variable m. In this equation, y and x are constant variables (they are always represented as y and x) and b is the y-intercept of the line.
We can do this by using the coordinates of the point and the slope formula given two coordinate points of a line:
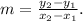
Therefore, because we defined our values earlier, we can substitute these into the equation and solve for m.
Our values were:
- x₁ = -1
- y₁ = 1
- x₂ = -1
- y₂ = 4
Therefore, we can substitute these values above and solve the equation.
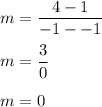
Therefore, we get a slope of zero, so we need to determine if this is a vertical line or a horizontal line. Therefore, we need to check to see if the x-coordinates are the same or if the y-coordinates are the same. We can easily check this.
x₁ = -1
x₂ = -1
y₁ = 1
y₂ = 4
If our y-coordinates are the same, the line is horizontal.
If our x-coordinates are the same, the line is vertical.
We see that our x-coordinates are the same, so we can determine that our line is a vertical line.
Therefore, finding that our slope is vertical, using our rules above, we can determine that our slope is undefined.