Answer:
See Explanation
Explanation:
The question is incomplete. However, the available details is enough to work out a solution.
Considering the first even number: 2
In this case, n = 1
The sum of the first even term is 2.
Represent the sum as a product:

Considering the first two even numbers: 2 and 4
In this case, n = 2
The sum of the first two even terms is 6
Represent the sum as a product:
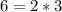
Considering the first three even numbers: 2, 4 and 6
In this case, n = 3
The sum of the first two even terms is 12
Represent the sum as a product:
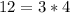
Notice the pattern from n = 1 to 3
 --- n = 1
--- n = 1
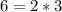 --- n = 2
--- n = 2
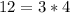 --- n = 3
--- n = 3
------------------------------------
It follows that, the sum when represented as a product is:
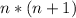
So, the sum of the first 52 even terms would be:
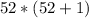
Where n = 52
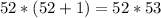
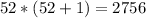
Hence, the sum of the first 52 even terms is 52 * 53 or 2756