Question

Derive the equation of the parabola with a focus at (−5, 5) and a directrix of y = −1.

f(x) = −one twelfth(x − 5)2 + 2
f(x) = one twelfth(x − 5)2 + 2
f(x) = −one twelfth(x + 5)2 + 2
f(x) = one twelfth(x + 5)2 + 2

Answer 1

The equation of the parabola with a focus at (-5,5) and a directrix of y = -1 is
`y = (1)/(12)\cdot (x+5)^(2)+2`.

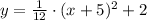Explanation:

From statement we understand that parabola has its axis of symmetry in an axis parallel to y-axis. According to Analytical Geometry, the minimum distance between focus and directrix equals to twice the distance between vertex and any of endpoints.

If endpoints are (-5, 5) and (-5, -1), respectively, then such distance (
`r`), dimensionless, is calculated by means of the Pythagorean Theorem:

`r = (1)/(2)\cdot \sqrt{[-5-(-5)]^(2)+[5-(-1)]^(2)}`

`r = 3`

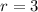
And the location of the vertex (
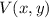`V(x,y)`), dimensionless, which is below the focus, is:

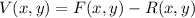`V(x,y) = F(x,y)-R(x,y)` (1)

Where:

`F(x,y)` - Focus, dimensionless.

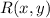`R(x,y)` - Vector distance, dimensionless.

If we know that
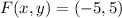`F(x,y) = (-5,5)` and
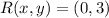`R(x,y) = (0,3)`, then the location of the vertex is:

`V(x,y) = (-5,5)-(0,3)`

`V(x,y) =(-5,2)`

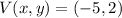
In addition, we define a parabola by the following expression:

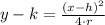`y-k = ((x-h)^(2))/(4\cdot r)` (2)

Where:

`h`,
`k` - Coordinates of the vertex, dimensionless.

`r` - Distance of the focus with respect to vertex, dimensionless.

If we know that
`h = -5`,
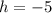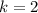`k = 2` and
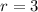`r = 3`, then the equation of the parabola is:

`y = (1)/(12)\cdot (x+5)^(2)+2`

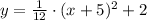
The equation of the parabola with a focus at (-5,5) and a directrix of y = -1 is
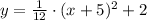`y = (1)/(12)\cdot (x+5)^(2)+2`.