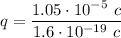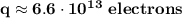Answer:
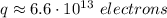
Step-by-step explanation:
Coulomb's Law
The force between two charged particles of charges q1 and q2 separated by a distance d is given by the Coulomb's Law formula:

Where:
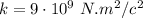
q1, q2 = the objects' charge
d= The distance between the objects
We know both charges are identical, i.e. q1=q2=q. This reduces the formula to:
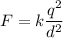
Since we know the force F=1 N and the distance d=1 m, let's find the common charge of the spheres solving for q:
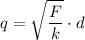
Substituting values:
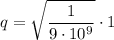
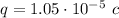
This charge corresponds to a number of electrons given by the elementary charge of the electron:
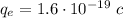
Thus, the charge of any of the spheres is: