Answer:
The new value after an increase
of £258 by 43 will be: 368.94
Explanation:
As we have to increase £258 by 43 using the multiplier method.
Let 'n' represent the new value after the increase of £258 by 43 using the multiplier method.
Using the formula
n = 258 + percentage increase
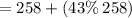
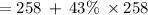
Factoring out 258
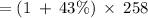
as 1 = 100 / 100 = 100%
so
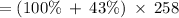
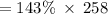
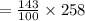
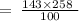
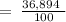
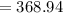
Therefore, the new value after an increase
of £258 by 43 will be: 368.94