Question

It is possible to get 2 solutions when the system of equations is: (check all that apply)

A system of 2 linear equations in 2 variables
A system of 3 linear equations in 3 variables
A system of the equation of a circle and a linear equation
A system of the equation of a parabola and a linear equation

Answer 1

A system of the equation of a circle and a linear equation

A system of the equation of a parabola and a linear equation

Explanation:

Let us verify our answer

A system of the equation of a circle and a linear equation

Let an equation of a circle as
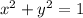`x^2+ y^2 = 1` ..........(1)

Let a liner equation Y = x ............(2)

substitute (2) in (1)

`x^2 + x^2 = 1\\2x^2 = 1\\`

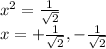`x^2 = (1)/(√(2) ) \\x = +(1)/(√(2) ) , -(1)/(√(2) )` so Y =
`+(1)/(√(2) ) , -(1)/(√(2) )`

so the two solution are (
`((1)/(√(2) ) ,(1)/(√(2) )) (-(1)/(√(2) ), -(1)/(√(2) )`)

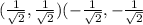A system of the equation of a parabola and a linear equation

Let equation of Parabola be
`y^2 = x`

and linear equation y = x

substitute

`x^2 = x\\x^2 - x= 0\\x(x-1) = \\x = 0 , 1`

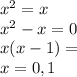
Y = 0,1

so the two solutions will be (0,0) and (1,1)