Question

A goat is tired to a pole at the center of a square of length of side 20m. If the rope is 10m long. Calculate the (I) area of the square that can't be grazed by the goat (ii) fraction of grazed portion to the whole area​

Answer 1

percentage = 78.54%

Explanation:

The area of a square of side length x is:

`A_s=x^2`

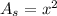
The area of a circle of radius r is:

`A_c=\pi r^2`

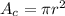
The goat is tied to a pole at the center of a square of a side length of x=20 cm.

The area of the square is:

`A_s=20^2`

`A_s=400~m^2`

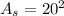
The rope is 10 m long. The goat is able to graze an area of:

`A_c=\pi 10^2`

`A_c=100\pi~m^2`

(i)

Since the diameter of the circle (20 m) is equal to the length of the square, the area of the circle is contained in the square and the area of the square not grazed by the goat is:

`A = A_s-A_c=400~m^2-100\pi~m^2`

`A=100(4-\pi)~m^2`

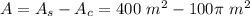
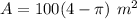
Calculating:

`A = 85.84~m^2`

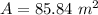
(ii)

The percentage can be calculated as:

`\displaystyle (A_c)/(A_s)*100=(100\pi)/(400)*100=25\pi`

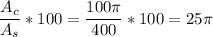
Calculating:

percentage = 78.54%