Answer:
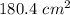
Explanation:
Surface Area
The surface area of a cylinder of height h and radius r is given by:

It only covers the lateral side of the cylinder. If both the top and the bottom sides are to be included, then:
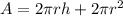
The label will cover only the lateral side of the soup can that has a height of h=8.5 cm and a diameter of 6.5 cm. We need to calculate the radius which is half of the diameter r=6.5 cm / 2 = 3.25 cm.
Now we calculate the side area of the can:


We need to add the 0.8 cm overlap to the total area already calculated. This overlap has 0.8 cm of width and 8.5 cm of height, so this overlap area is:
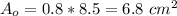
The total area of the label is:
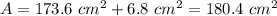
The area of the label is
