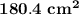Question

The part of a cylindrical soup can that is covered by the label is 8.5 cm tall and has a diameter of 6.5 cm. What is the area of a label that covers the entire side of the can and that need a 0.8-cm overlap to glue the ends of the label? Round to the nearest tenth.

Answer 1

`180.4~cm^2`

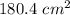
Explanation:

Surface Area

The surface area of a cylinder of height h and radius r is given by:

`A=2\pi rh`

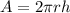
It only covers the lateral side of the cylinder. If both the top and the bottom sides are to be included, then:

`A=2\pi rh+2\pi r^2`

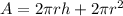
The label will cover only the lateral side of the soup can that has a height of h=8.5 cm and a diameter of 6.5 cm. We need to calculate the radius which is half of the diameter r=6.5 cm / 2 = 3.25 cm.

Now we calculate the side area of the can:

`A=2\pi (3.25)(8.5)`

`A=173.6~cm^2`

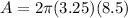
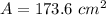
We need to add the 0.8 cm overlap to the total area already calculated. This overlap has 0.8 cm of width and 8.5 cm of height, so this overlap area is:

`A_o= 0.8*8.5=6.8~cm^2`

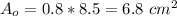
The total area of the label is:

`A=173.6~cm^2+6.8~cm^2=180.4~cm^2`

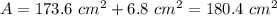
The area of the label is
`\mathbf{180.4~cm^2}`