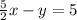Answer:
- The equation in slope-intercept form is
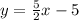
- The equation in the standard form will be:
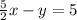
Explanation:
- The x-intercept is obtained when we set the value y=0
As the x-intercept is 2, therefore the point representing
the x-intercept will be: (2, 0)
- The y-intercept is obtained when we set the value x=0
As the y-intercept is -5, therefore the point representing
the y-intercept will be: (0, -5)
So we get the two points
(2, 0)
(0, -5)
Finding the slope between (2, 0) and (0, -5)
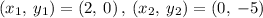
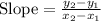
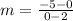
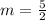
Using the point-slope form of the line equation

Here m is the slope
substituting the values m = 5/2 and the point (2, 0)
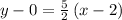
so writing the equation in slope-intercept form
As we know that the slope-intercept form is

here
so
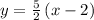
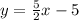
Hence, the equation in slope-intercept form is
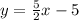
Writing the equation in the standard form form
As we know that the equation in the standard form is
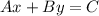
where x and y are variables and A, B and C are constants
As we already know the equation in slope-intercept form
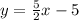
so the equation in the standard form will be: