Question

Question 6 (1.25 points)

A researcher wants to test if the mean annual salary of all lawyers in a city is
different from $110,000. A random sample of 53 lawyers selected from the city
reveals a mean annual salary of $114,000. Assume that o = $17,000, and that the
test is to be made at the 1% significance level.
What is the value of the test statistic, z, rounded to three decimal places?
A

Answer 1

Test statistic Z= 1.713

The calculated Z- value = 1.7130 < 2.576 at 0.01 level of significance

Null hypothesis is accepted

There is no difference between the mean annual salary of all lawyers in a city is different from $110,000

Explanation:

Step(i):-

A researcher wants to test if the mean annual salary of all lawyers in a city is

different from $110,000

Mean of the Population μ = $110,000

Sample size 'n' = 53

Mean of the sample x⁻ = $114,000.

standard deviation of the Population = $17,000,

Level of significance = 0.01

Null hypothesis :

There is no difference between the mean annual salary of all lawyers in a city is different from $110,000

H₀: x⁻ = μ

Alternative Hypothesis : x⁻ ≠ μ

Step(ii):-

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (114000-110000)/((17000)/(√(53) ) )`

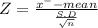
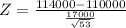
Z = 1.7130

Tabulated value Z = 2.576 at 0.01 level of significance

The calculated Z- value = 1.7130 < 2.576 at 0.01 level of significance

Null hypothesis is accepted

There is no difference between the mean annual salary of all lawyers in a city is different from $110,000