Question

Heres an ez question for yall

Which of the following sets could be the sides of a right triangle
{5, 8, 12}
{3, 5,
`\sqrt\\ 34` }
{2, 3,
`\sqrt{} 34` }

Answer 1

Answer: Choice B

`\left\{ \ 3, 5, √(34) \ \right\}`

=========================================================

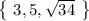
Step-by-step explanation:

We'll be using the converse of the pythagorean theorem.

If we had a triangle with sides a,b,c and
`a^2+b^2 = c^2` was true, then we have a right triangle. Note: c is always the longest side

For the first answer choice we have: a = 5, b = 8, c = 12

Then,

`a^2+b^2 = c^2\\\\5^2+8^2 = 12^2\\\\25+64 = 144\\\\89 = 144\\\\`

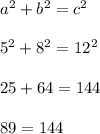
which is false. This shows that we do not have a right triangle with sides 5,8,12. This rules out choice A. Choice C is a similar story.

Choice B on the other hand works because

`a^2+b^2 = c^2\\\\3^2+5^2 = (√(34))^2\\\\9+25 = 34\\\\34 = 34\\\\`

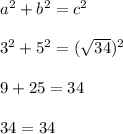
We have a true statement at the end, which confirms choice B is a right triangle.