Question

(04.04 LC)

On a coordinate grid, point T is at (2,-4) and point Sis at (2,6). The distance (in units) between points T and Sis
numbers, such as 2.) (5 points)
(Input only whole

Answer 1

t and s

Explanation:

Answer 2

The distance 'd' between T and S:

• 
  `d=10`

Explanation:

As the point 'T' is located at (2, -4)

• So, the point 'T' has the coordinates (2, -4)

And the point 'S' is located at (2, 6)

• So, the point 'T' has the coordinates (2, 6)

The distance 'd' between T and S can be computed using the formula:

`d=√(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

`=√(\left(2-2\right)^2+\left(6-\left(-4\right)\right)^2)`

`=√(\left(2-2\right)^2+\left(6+4\right)^2)`

`=√(0+10^2)`

`=√(10^2)`

`d=10`

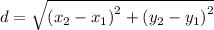
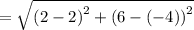
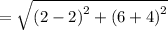
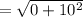
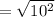
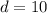
Therefore, the distance 'd' between T and S:

• 
  `d=10`