Question

A pool that is being drained contained 18,000 gallons of water. After 2 hours, 12, 500

Gallons of water remain. Write an equation in all 3 forms to model this situation,
HELLPPP PLLEASEEEE!!!!!

Answer 1

y-18,000=2,750(x-0) --> point-slope

y=2,750x+18,000 --> slope-intercept

-2,750x + y = 18,000 --> standard

Explanation:

Linear Modeling

Some situations can be modeled as linear functions. If we are in a situation where a linear model is suitable, then we need two sample points to make the model and predict unknown behaviors.

The pool being drained contained initially 18,000 gallons of water. If we set the variable x as the time in hours and y as the remaining gallons of water in the pool, this first point is (0;18,000).

We are also aware that after 2 hours 12,500 gallons of water remain. This gives us the second point as (2;12,500).

The equation of a line passing through points (x1,y1) and (x2,y2) can be found as follows:

`\displaystyle y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

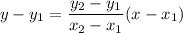
Let's find the equation of the line with the 2 points:

`\displaystyle y-18,000=(18,000-12,500)/(2-0)(x-0)`

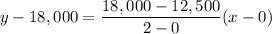
Calculating:

`\displaystyle y-18,000=(5,500)/(2)(x-0)`

`y-18,000=2,750(x-0)`

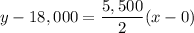
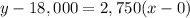
The equation above is the point-slope form of the line

Simplifying and adding 18,000:

`y=2,750x+18,000`

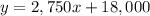
The equation above is the slope-intercept form of the line

Moving all the variables to the left side:

`-2,750x + y = 18,000`

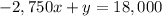
The equation above is the standard form of the line

Answer:

y-18,000=2,750(x-0) --> point-slope

y=2,750x+18,000 --> slope-intercept

-2,750x + y = 18,000 --> standard