The question does not clearly specify from which endpoint Q is at 2/3. I'll assume Q is 2/3 away from R.
Answer:
The point Q is (2,3)
Explanation:
Take the aligned points R(-2,1), S(4,4), and Q(x,y) in such a way that Q is 2/3 away from R (assumed).
The required point Q must satisfy the relation:
d(RQ) = 2/3 d(RS)
Where d is the distance between two points.
The horizontal and vertical axes also satisfy the same relation:
x(RQ) = 2/3 x(RS)
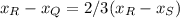
And, similarly:
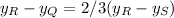
Working on the first condition:
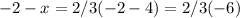
Removing the parentheses:
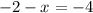
Adding 2:
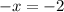
x = 2
Similarly, working with the vertical component:

Removing the parentheses:
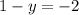
Subtracting 1:
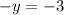
y = 3
The point Q is (2,3)