Answer:
The coordinates of point X that divides the line in 1:4 are: (3,8/5)
Explanation:
When a point divides a line with coordinates (x1,y1) and (x2,y2) in ratio m:n,
the coordinates of point are given by:
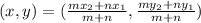
Given points are:
(x1,y1) = (5,1)
(x2,y2) = (-5,4)
Putting the values in the formula
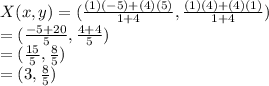
Hence,
The coordinates of point X that divides the line in 1:4 are: (3,8/5)