Question

Suppose a car that sells for $40,000 depreciates 10% per year. How many

years would it take for the car to have a value less than $25,000?

Answer 1

It would take 5 years for the car to have a value of less than $25,000

Explanation:

Exponential Decaying Model

The exponential function is often used to model natural decaying processes, where the change is proportional to the actual quantity.

We have the initial value of a car is $40,000. Each year it depreciates by 10%.

Thus the first year its value is 90% of the initial value:

V1 = 90 * $40,000 / 100 = $36,000

By the second year its value is 90% of $36,000:

V2 = 90 * $36,000 / 100 = $32,400

Note the value for a year n is the original value multiplied by 90% (or 0.9) to the power of n:

`Vn = $40,000 \cdot 0.9^n`

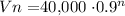
To find the number of years needed to have a value of less than $25,000, we solve the equation:

`40,000 \cdot 0.9^n = 25,000`

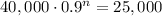
Dividing by 40,000:

`0.9^n = 25,000/40,000 = 0.625`

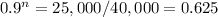
Taking logarithms:

`n\log 0.9=\log 0.625`

`n=\log 0.625 / \log 0.9`

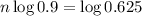
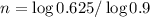
n =4.5

We'll round up to n = 5

It would take 5 years for the car to have a value of less than $25,000