Question

Your field experience instructor wants to line up 7 cars for transportation to a grade school. Between you and your classmates, there are 29 cars available. How many different groups of 7 cars are possible? different groups

Answer 1

1560780 selections

Explanation:

Given

Cars = 29

Selection = 7

Required

Possible number of selections

The interpretation of the question is that, in how many ways can 7 cars be selected from 29.

This is done using combination formula as follows:.

`^nC_r = (n)/((n-r)!r!)`

Where

`n = 29`

`r = 7`

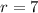
So, the formula becomes:

`^(29)C_7 = (29!)/((29-7)!7!)`

`^(29)C_7 = (29!)/(22!7!)`

`^(29)C_7 = (29*28*27*26*25*24*23*22!)/(22!7!)`

`^(29)C_7 = (29*28*27*26*25*24*23)/(7!)`

`^(29)C_7 = (29*28*27*26*25*24*23)/(7*6*5*4*3*2*1)`

`^(29)C_7 = (7866331200)/(5040)`

`^(29)C_7 = 1560780`

Hence, the number of ways is 1560780