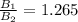Answer:
The ratio is
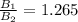
Step-by-step explanation:
From the question we are told that
The density of fresh water is

The density of ethanol is
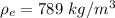
Generally speed of a wave in a substance is mathematically represented as
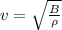
Here B is the adiabatic bulk modulus of the substance while
 is the density of the substance
is the density of the substance
So at constant wave speed
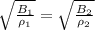
=>
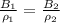
=>
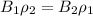
=>
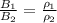
Here
 and
and
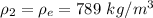
So
=>

=>