9514 1404 393
Answer:
a) f: all real numbers except 1 and 2; g: all real numbers except 2
b) f(x) = 5/(x -2) . . . . x = 2 is a vertical asymptote
c) f(x) = -5/4, -5/3, -5/2, undefined, undefined, 5, 5/2
g(x) = -5/4, -5/3, -5/2, -5, undefined, 5, 5/2
d) f(x) is also undefined at x=1
Explanation:
a) Any question about the domain of a function concerns the values of the variable for which the function is defined, or not. A rational function, such as these, will be undefined when its denominator is zero. So the question of domain becomes a question of the values of x that make the denominator zero.
The zeros of the denominator of f(x) can be found by factoring it.
x^2 -3x +2 = (x -1)(x -2)
These factors are zero when x=1 and when x=2. Hence, these values are excluded from the domain of f(x).
domain of f(x): all real numbers except x=1 and x=2
Then, by inspection, the domain of g is similar, but a little different:
domain of g(x): all real numbers except x=2
__
b) Based on our work for part (a), we find that f(x) can be factored and simplified like this.
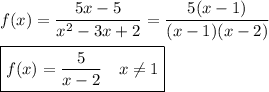
There will be a vertical asymptote at x=2. The attachment shows a graph of f(x) with its vertical asymptote.*
__
c) The difference between the two functions is that f(x) is undefined at x=1.
x = -2, -1, 0, 1, 2, 3, 4
f(x) = -5/4, -5/3, -5/2, undef, undef, 5, 5/2
g(x) = -5/4, -5/3, -5/2, -5, undef, 5, 5/2
__
d) The functions differ in that f(x) is undefined at x=1, whereas g(x) is not.
_____
* The fact that f(x) is undefined at x=1, but there is no vertical asymptote at that point, means the function has a "hole" in its graph there. This is illustrated on the graph by an open circle, meaning the function is not defined at that point.