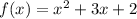Question

Write the equation of the quadratic function whose graph passes through
`(-3,2)`,
`(-1,0)`, and
`(1,6)`.

Answer 1

`f(x)=x^2+3x+2`

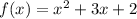
Explanation:

We want to write the equation of a quadratic whose graph passes through (-3, 2), (-1, 0), and (1, 6).

Remember that the standard quadratic function is given by:

`f(x)=ax^2+bx+c`

Since it passes through the point (-3, 2). This means that when
`x=-3`,
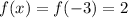`f(x)=f(-3)=2`. Hence:

`f(-3)=2=a(-3)^2+b(-3)+c`

Simplify:

`2=9a-3b+c`

Perform the same computations for the coordinates (-1, 0) and (1, 6). Therefore:

`0=a(-1)^2+b(-1)+c \\ \\0=a-b+c`

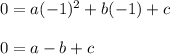
And for (1, 6):

`6=a(1)^2+b(1)+c\\\\ 6=a+b+c`

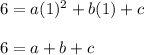
So, we have a triple system of equations:

`\left\{ \begin{array}{ll} 2=9a-3b+c &\\ 0=a-b+c \\6=a+b+c \end{array} \right.`

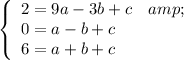
We can solve this using elimination.

Notice that the b term in Equation 2 and 3 are opposites. Hence, let's add them together. This yields:

`(0+6)=(a+a)+(-b+b)+(c+c)`

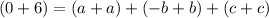
Compute:

`6=2a+2c`

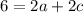
Let's divide both sides by 2:

`3=a+c`

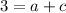
Now, let's eliminate b again but we will use Equation 1 and 2.

Notice that if we multiply Equation 2 by -3, then the b terms will be opposites. So:

`-3(0)=-3(a-b+c)`

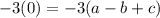
Multiply:

`0=-3a+3b-3c`

Add this to Equation 1:

`(0+2)=(9a-3a)+(-3b+3b)+(c-3c)`

Compute:

`2=6a-2c`

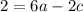
Again, we can divide both sides by 2:

`1=3a-c`

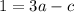
So, we know have two equations with only two variables:

`3=a+c\text{ and } 1=3a-c`

We can solve for a using elimination since the c term are opposites of each other. Add the two equations together:

`(3+1)=(a+3a)+(c-c)`

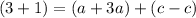
Compute:

`4=4a`

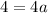
Solve for a:

`a=1`

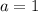
So, the value of a is 1.

Using either of the two equations, we can now find c. Let's use the first one. Hence:

`3=a+c`

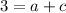
Substitute 1 for a and solve for c:

`\begin{aligned} c+(1)&=3 \\c&=2 \end{aligned}`

So, the value of c is 2.

Finally, using any of the three original equations, solve for b:

We can use Equation 3. Hence:

`6=a+b+c`

Substitute in known values and solve for b:

`6=(1)+b+(2)\\\\6=3+b\\\\b=3`

Therefore, a=1, b=3, and c=2.

Hence, our quadratic function is:

`f(x)=x^2+3x+2`