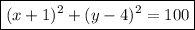a)
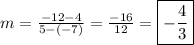
b) We know the equation is
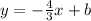 , where b is a constant. If we substitute in the coordinates of point a, we get that:
, where b is a constant. If we substitute in the coordinates of point a, we get that:
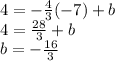
This means the y-intercept is
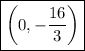
To find the x-intercept, we can set the equation equal to 0 and solve for x.
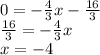
So, the x-intercept is
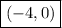
c)
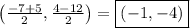
d)
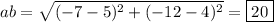
e) The perpendicular bisector must pass through the midpoint, (-1, 4), and have a slope that is the negative reciprocal (so in this case, 3/4). Substituting into point-slope form,
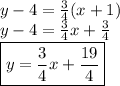
f) If ab is a diameter of said circle, this means it is centered at the midpoint, (-1, 4), and has a radius of 20/2=10. This means the equation is