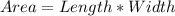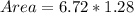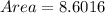Answer:
1.
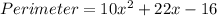
2.
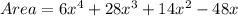
3.
 or
or

4.
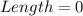 and
and
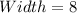
5.
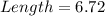 and
and
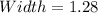
6. Second Solution
7.
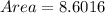
Explanation:
Given
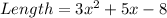
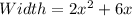
Solving (1): The perimeter
Perimeter is calculated as thus:

Substitute values for Length and Width
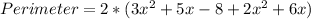
Collect Like Terms
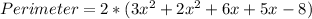
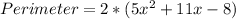
Open Bracket
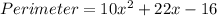
Solving (2): The Area:
Area is calculated as thus:
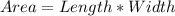
Substitute values for Length and Width
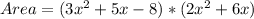
Expand Bracket

Open Bracket
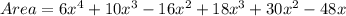
Collect Like Terms
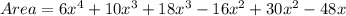
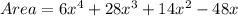
Solving (3): If perimeter is 16, show that x = 1 and x = -3.2
In (a)
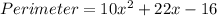
Substitute 16 for Perimeter
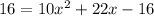
Equate to 0
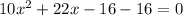

Expand
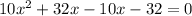
Factorize
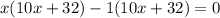
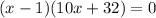
Split
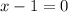 or
or

 or
or
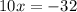
 or
or
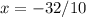
 or
or

Solving (4): Using x = 1; Solve the dimension of the rectangle
We have that:
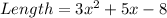
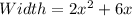
Substitute 1 for x in the given parameters
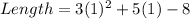

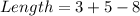
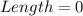
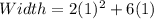


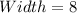
Solving (5): Using x = -3.2; Solve the dimension of the rectangle
We have that:
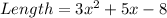
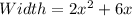
Substitute -3.2 for x in the given parameters
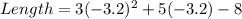

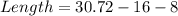
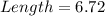
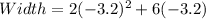
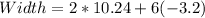
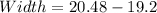
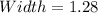
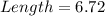 and
and
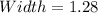
Solving (6):
In the first solution of the dimensions in number 4, we have that
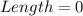 and
and
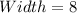
This dimension can not be considered because the length of a rectangle can not be 0
In the second solution of the dimensions in number 5, we have that
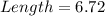 and
and
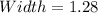
This dimension makes more sense because both dimensions are greater than 0
Solving (7): Using (6), determine the Area
In (6), we conclude that
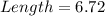 and
and
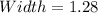
So, Area is calculated as thus: