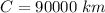Answer:
The circumference of planet tirth is
Step-by-step explanation:
From the question we are told that
The distance of tyene from the observer is
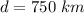
The altitude of the sun from the equinox is

Generally given that on the equinox your sun is directly overhead in the city of tyene , then the altitude of the tyene from the equinox is
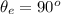
Generally the angular distance between tyene and the sun as observed from the equinox is mathematically represented as
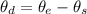
=>
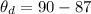
=>
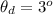
Generally the ratio of
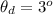 to
to
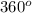 which is the total angle in a circle is equal to the ratio of
which is the total angle in a circle is equal to the ratio of
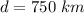 to the circumference of the planet
to the circumference of the planet
So
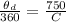
=>
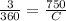
=>