Question

A and B are postive integers such that 1/a + 1/b +1/ab = 1. Find ab

Answer 1

Answer: ab =6

have:

`(1)/(a)+(1)/(b)+(1)/(ab)=1\\\\=>(b)/(ab)+(a)/(ab)+(1)/(ab)=1\\\\<=>(a+b+1)/(ab)=1`

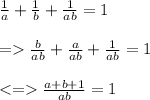
=> a + b + 1 = ab

⇔ a + b + 1 - ab = 0

⇔ b - 1 - a(b - 1) + 2 = 0

⇔ (b - 1)(1 - a) = -2

because a and b are postive integers => (b - 1) and (1 - a) also are integers

=> (b - 1) ∈ {-1; 1; 2; -2;}

(1 -a) ∈ {-1; 1; 2; -2;}

because (b -1).(1-a) = -2 => we have the table:

b - 1 -1 1 2 -2

1 - a 2 -2 -1 1

a -1 3 2 0

b 0 2 3 -1

a.b 0 6 6 0

because a and b are postive integers

=> (a;b) = (3;2) or (a;b) = (2;3)

=> ab = 6

Explanation: