Answer:
The surface area of the rectangular box is
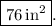
Step-by-step explanation:
The surface area of a rectangular box is the sum of the areas of its six faces. In this case, we have three pairs of opposite faces with equal dimensions. The dimensions of the box are given as 4"×2"×5". Each pair of opposite faces contributes twice to the total surface area. Therefore, the surface area (\(A_{\text{total}}\)) can be calculated using the formula:
![\[ A_{\text{total}} = 2(lw + lh + wh) \]](https://img.qammunity.org/2023/formulas/mathematics/college/neb6k187zdauj0m09s7tbrt3h5ih1tcm8q.png)
Substituting the given values, where
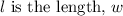 is the width, and \( h \) is the height:
is the width, and \( h \) is the height:
![\[ A_{\text{total}} = 2(4 * 2 + 4 * 5 + 2 * 5) \]](https://img.qammunity.org/2023/formulas/mathematics/college/opw1fjos9itb4zsdqlffnh1nk43e7k4jg7.png)
Simplifying this expression gives us the final answer. The units for the surface area are square inches
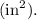 Therefore, the calculated surface area for the given rectangular box is
Therefore, the calculated surface area for the given rectangular box is
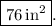
In conclusion, understanding the geometry of the box and utilizing the surface area formula allows us to determine the total surface area efficiently. The final result,
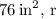 epresents the amount of material needed to manufacture the rectangular box to hold teabags.
epresents the amount of material needed to manufacture the rectangular box to hold teabags.