Question

Consider the series ​

[infinity]
∑ (-1)^n (x+1)^n/ (n+1)!
n=0

a. Find the​ series' radius and interval of convergence. ​
b. For what values of x does the series converge​ absolutely?
c. For what values of x does the series converge​ coditionally?

Answer 1

(a) If

`f(x)=\displaystyle \sum_(n=0)^\infty (-1)^n ((x+1)^n)/((n+1)!)`

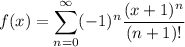
then by the ratio test, the series converges for all x, since

`\displaystyle \lim_(n\to\infty) \left| ( (-1)^(n+1) ((x+1)^(n+1))/((n+2)!) )/( (-1)^n ((x+1)^n)/((n+1)!) ) \right|=\lim_(n\to\infty)(|x+1|)/(n+2)=0`

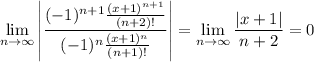
so the series radius of convergence is ∞ and the interval of convergence is (-∞, ∞).

(b) The series converges everywhere absolutely, because the ratio test for

`\displaystyle \sum_(n=0)^\infty (|x+1|^n)/((n+1)!)`

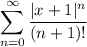
also shows the radius of convergence is ∞.

(c) The series converges absolutely, so conditional convergence is moot.