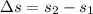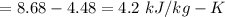Question

A rigid, insulated vessel is divided into two equal-volume compartments connected by a valve. Initially, one compartment con tains 1 m3 of water at 20°C, x = 50%, and the other is evacuated. The valve is opened and the water is allowed to fill the entire volume. For the water, determine the final temperature, in °C, and the amount of entropy produced, in kJ/K.

Answer 1

Given

Volume,
`$V_1 = 1 \ m^3$`

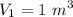
Temperature,
`$T_1=20 \ ^\circ C`

`$x_1=0.5$`

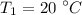
From the saturated water table, corresponding to
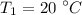`$T_1=20 \ ^\circ C`, we get the saturated liquid, vapor specific and the entropy.

`$v_f=1.0010 \ m^3/kg$`

`$v_g=57.791 \ m^3/kg$`

`$s_f=0.2966 \ kJ/kg-K$`

`$s_g=8.6672 \ kJ/kg-K$`

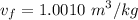
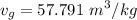
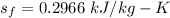
Now calculating the initial specific volume

`$v_1=v_f+x_1 \cdot(v_g-v_f)$`

`$=1.0018+05 \cdot(57.791-1.0018)$`

`$= 29.8973 \ m^3/kg$`

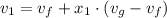
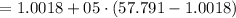
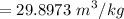
Calculating the initial specific entropy:

`$s_1=s_f+x+1 \cdot (s_g-s_f)$`

`$=0.2966+0.5 \cdot (8.6673 - 0.2966)$`

`$= 4.48 \ kJ/kg-K$`

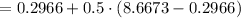
So final volume of the vessel is two times bigger as the initial volume

`$V_2=2 .V_1$`

`$= 2 * 29.8973 = 59.8 \ m^3/kg$`

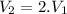
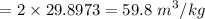
If we interpolate the values from tables between
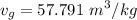`$v_g=57.791 \ m^3/kg$` and
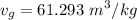`$v_g=61.293 \ m^3/kg$`, we can get final temperature and specific entropy corresponding to value of
`$v_2$` :

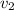Final temperature,
`$T_2= 19.6 ^\circ C$`

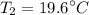
and
`$s_2 = 8.68 \ kJ/kg-K$`

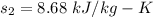
Calculating change in entropy

`$\Delta s = s_2-s_1$`

`$=8.68-4.48 = 4.2 \ kJ/kg-K$`