Answer: 2.81%
Step-by-step explanation:
If the abundance of Fe-56 is 91.75%, then the other two isotopes have a combined abundance of 100%-91.75%=8.25%.
If we let the abundance of Fe-54 be x, then the abundance of Fe-57 is 0.0825-x. Substituting this into the atomic mass formula, we get:
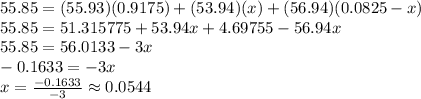
If x=0.1633/3, this means that 0.0825-x=0.0281, so Fe-57 is the rarest isotope, with an abundance of 2.81%