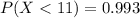Answer:
When the sample size is
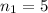 ,
,
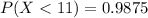
When the sample size is
 ,
,
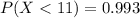
Explanation:
From the question we are told that
The mean is

The standard deviation is
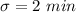
The first sample size is
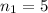
The second sample size is

Generally the standard error of the mean is mathematically represented as
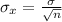
=>
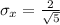
When the sample size is
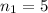 ,
,
Generally the standard error of the mean is mathematically represented as
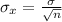
=>
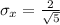
=>
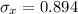
Generally the probability that the sample average amount of time taken on each day is at most 11 min is mathematically represented as
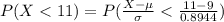
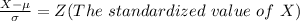

From the z table the area under the normal curve to the left corresponding to 2.24 is
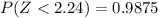
=>
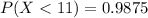
When the sample size is
 ,
,
Generally the standard error of the mean is mathematically represented as
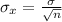
=>
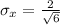
=>
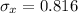
Generally the probability that the sample average amount of time taken on each day is at most 11 min is mathematically represented as
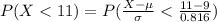
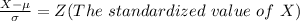

From the z table the area under the normal curve to the left corresponding to 2.24 is

=>