Question

Working together, Candice and Ximena painted a fence in 8 hours. Last year, Ximena painted the fence by herself. The year before, Candice painted it by herself, but took 12 hours less than Ximena took. How long did Candice and Ximena take, when each was painting alone?

Answer 1

Answer: Time taken by Ximena to paint the fence alone = 24 hours

Time taken by Candice to paint the fence alone = 12 hours

Explanation:

Let x= Time taken by Ximena to paint the fence alone .

Time taken by Candice to paint the fence alone = x-12

As per given , we have

`(1)/(x)+(1)/(x-12)=(1)/(8)\\\\\Rightarrow\ (x-12+x)/(x(x-12))=(1)/(8)\\\\\Rightarrow\ 8(2x-12)=x^2-12x\\\\\Rightarrow\ 16x-96=x^2-12x\\\\\Rightarrow\ x^2-12x-16x+96=0\\\\\Rightarrow\ x^2-28x+96=0\\\\\Rightarrow\ x^2-4x-24x+96=0\\\\\Rightarrow\ x(x-4)-24(x-4)=0\\\\\Rightarrow\ (x-4)(x-24)=0\\\\\Rightarrow x=4, 24`

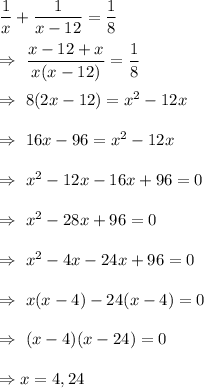
if x= 4

Time taken by Ximena = 4 hours

Time taken by Candice = 4-12 hours =-8 hours which is not possible. (time cannot be negative)

Therefore, x= 24

Such that

Time taken by Ximena to paint the fence alone = 24 hours

Time taken by Candice to paint the fence alone = 24-12=12 hours