Answer:
a) The horizontal asymptote of
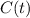 is
is
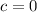 .
.
b) When t increases, both the numerator and denominator increases, but given that the grade of the polynomial of the denominator is greater than the grade of the polynomial of the numerator, then the concentration of the drug converges to zero when time diverges to the infinity. There is a monotonous decrease behavior.
c) The time at which the concentration is highest is approximately 1.291 hours after injection.
Explanation:
a) The horizontal asymptote of
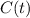 is the horizontal line, to which the function converges when
is the horizontal line, to which the function converges when
 diverges to the infinity. That is:
diverges to the infinity. That is:
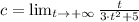 (1)
(1)
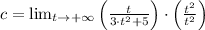
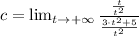
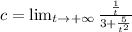
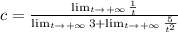
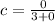
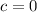
The horizontal asymptote of
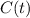 is
is
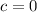 .
.
b) When t increases, both the numerator and denominator increases, but given that the grade of the polynomial of the denominator is greater than the grade of the polynomial of the numerator, then the concentration of the drug converges to zero when time diverges to the infinity. There is a monotonous decrease behavior.
c) From Calculus we understand that maximum concentration can be found by means of the First and Second Derivative Tests.
First Derivative Test
The first derivative of the function is:
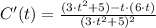

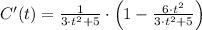
Now we equalize the expression to zero:
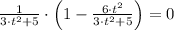
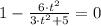
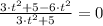
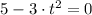
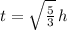
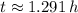
The critical point occurs approximately at 1.291 hours after injection.
Second Derivative Test
The second derivative of the function is:
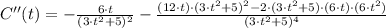
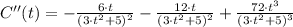
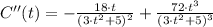
If we know that
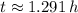 , then the value of the second derivative is:
, then the value of the second derivative is:
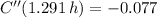
Which means that the critical point is an absolute maximum.
The time at which the concentration is highest is approximately 1.291 hours after injection.