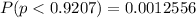Answer:
The probability is
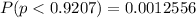
Explanation:
From the question we are told
The population proportion is
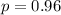
The sample size is
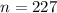
The number of graduate who had job is k = 209
Generally given that the sample size is large enough (i.e n > 30) then the mean of this sampling distribution is
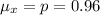
Generally the standard deviation of this sampling distribution is
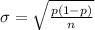
=>
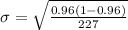
=>
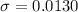
Generally the sample proportion is mathematically represented as
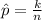
=>
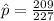
=>
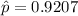
Generally probability of obtaining a sample proportion as low as or lower than this, if the university’s claim is true, is mathematically represented as
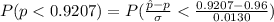

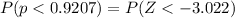
From the z table the area under the normal curve to the left corresponding to -3.022 is
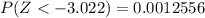
=>