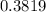Question

A standard deck of cards is​ purchased, and the deck includes 3 jokers. This means if the jokers are​ included, the deck contains 5 5 cards. Teresa is playing a game in which she is dealt 8 cards from a deck that includes the jokers. What is the probability that​ Teresa's hand includes at least one​ joker?

Answer 1

The probability is
`0.3819`

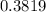
Explanation:

We know that Teresa is playing a game in which she is dealt 8 cards from a deck that includes 3 jokers and 52 common cards (a total of 55 cards).

Let's define the following random variable :

`X` : '' Number of jokers in the hand of Teresa ''

We need to find
`P(X\geq 1)`

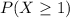
This probability is equivalent to :

`P(X\geq 1)=1-P(X=0)`

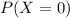`P(X=0)` is the probability of having none jokers in the 8 card hand.

In order to find
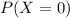`P(X=0)` we are going to count all the cases in which
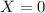`X=0` (given that we are in presence of an equally - likely sample space)

We calculate
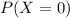`P(X=0)` as :

`P(X=0)=\frac{\left(\begin{array}{c}52&8\end{array}\right)\left(\begin{array}{c}3&0\end{array}\right)}{\left(\begin{array}{c}55&8\end{array}\right)}`

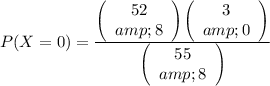
We define the combinatorial number
`nCr=\left(\begin{array}{c}n&r\end{array}\right)=(n!)/(r!(n-r)!)`

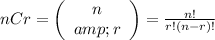
In the denominator we have
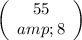`\left(\begin{array}{c}55&8\end{array}\right)` which represents all the ways in which we can extract 8 cards from the deck of 55 cards.

In the numerator we have the product of
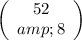`\left(\begin{array}{c}52&8\end{array}\right)` (which represents all the ways in which we can choose 8 cards from the 52 common cards) and
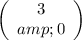`\left(\begin{array}{c}3&0\end{array}\right)` (which represents that from the total of 3 jokers we extract 0)

If we perform the operation we find that :

`P(X=0)=0.6181`

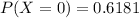
Finally,

`P(X\geq 1)=1-P(X=0)=1-0.6181=0.3819`

The probability is
`0.3819`