Question

A car turns from a road into a parking lot and into an available parking space. The car's initial velocity is 4 m/s [E 45° N]. The car's velocity just before the driver decreases speed is 4 m/s [E 10° N]. The turn takes 3s. What's the average acceleration of the car during the turn? The answer should have directions with an angle.

Answer 1

Step-by-step explanation:

From the given information:

The car's initial velocity = 4 m/s in the direction of east 45° due north

We can therefore express the vector of this component form as:

v₁ = (4 m/s) (cos(45º)i + sin(45º)j)

v₁ = (2.83 m/s)i + (2.83 m/s)j

Similarly, the car's final velocity = 4 m/s in the direction of the east side 10º north

∴

v₂ = (4 m/s) (cos(10º) i + sin(10º) j)

v₂ = (3.94 m/s) i + (0.695 m/s) j

From the first equation of motion

v = u + at

Making acceleration "a" the subject of the formula, we have:

a = (v - u )/t

a = (v₂ - v₁)/t

a = (0.370 m/s²) + (-0.711 m/s²)

The magnitude of the avg. acceleration is:

`|| a||= \sqrt{(0.370 m/s^2)^2 + (-0.711 m/s^2)^2)`

`|| a||= 0.8015 \ m/s^2`

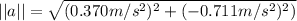
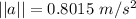
And;

The direction can be determined by taking the tangent of the acceleration:

i.e.

`tan(\theta) = (-0.711 m/s^2)/( 0.370 m/s^2)`

`tan(\theta) = -1.9216`

`\theta = tan^(-1) ( -1.9216 )`

`\mathbf{\theta = -62.51 ^0}`

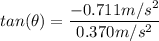
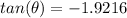
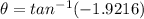
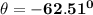
Thus, the direction of the angle is approximately S 62.51º E