Question

En una hoja de papel cuyo perímetro es de 96 centímetros, se quiere imprimir un volante de manera que el área impresa sea un rectángulo cuyo largo mida el doble del ancho, el margen superior mida 3 centímetros, el izquierdo 5 centímetros y los márgenes inferior y derecho midan 2 centímetros cada uno. ¿Cuál es el perímetro de la región impresa?, ¿cuál es el área?

Answer 1

El perímetro de la región impresa es 72 cm y su área es 288 cm².

Explanation:

1. Tenemos el perímetro de la hoja de papel:

P₁ = 96 cm = 2l₁ + 2a₁ (1)

Como sabemos el margen superior, inferior, izquierdo y derecho podemos encontrar la relación entre el largo y ancho del rectángulo interno (región impresa) con el largo (l) y ancho (a) del rectángulo externo (hoja de papel):

`l_(2) = l_(1) - (m_(s) + m_(i)) = l_(1) - (3 cm + 2 cm) = l_(1) - 5 cm` (2)

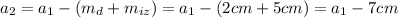`a_(2) = a_(1) - (m_(d) + m_(iz)) = a_(1) - (2 cm + 5 cm) = a_(1) - 7 cm` (3)

El perímetro del rectángulo interno es:

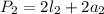`P_(2) = 2l_(2) + 2a_(2)` (4)

Introduciendo la ecuación (2) y (3) en (4):

`P_(2) = 2l_(2) + 2a_(2) = 2(l_(1) - 5 cm) + 2(a_(1) - 7 cm) = 2l_(1) + 2a_(1) - 10 cm - 14 cm = 96 cm - 24 cm = 72 cm`

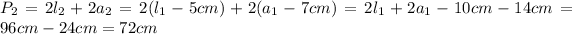
Por lo tanto el perímetro del rectángulo interno (región impresa) es 72 cm.

2. Ahora para encontrar el área rectángulo interno debemos encontrar el largo y ancho del mismo, sabiendo que:

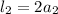`l_(2) = 2a_(2)` (5)

Introduciendo (5) en (4):

`P_(2) = 2l_(2) + 2a_(2) = 2*2a_(2) + 2a_(2) = 6a_(2)`

`a_(2) = (P_(2))/(6) = (72 cm)/(6) = 12 cm`

`l_(2) = 2a_(2) = 2*12 cm = 24 cm`

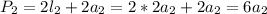
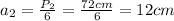
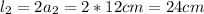
Entonces el área es:

`A_(2) = l_(2)*a_(2) = 12 cm*24 cm = 288 cm^(2)`

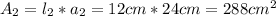
Por lo tanto el área del rectágulo interno (región impresa) es 288 cm².

Espero que te sea de utilidad!