Answer:
6 number treat sacks and
each sack having 5 pencils and 7 smiley face stickers.
Explanation:
Given that:
Number of pencils = 30
Number of smiley face stickers = 42
Mrs. MaryAnn wants to divide everything in identical treat sacks so that there are no leftovers.
To find:
The number of greatest number of treat sacks.
Solution:
First of all, we need to find the Highest Common Factor of the two numbers.
Factorization method:
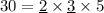
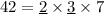
Here, the common numbers 2 and 3.
So, highest common factor is
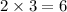
If we divide 30 by 6, we get 5 and
If we divide 42 by 6, we get 7
So, if we take 5 pencils and 7 smiley face stickers in one treat sack and if we make 6 such treat sacks then there will be equal division and no leftovers.
Therefore, the answer is:
6 number treat sacks and
each sack having 5 pencils and 7 smiley face stickers.