Answer:
i)
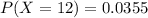
ii)
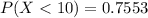
iii)

Explanation:
Let's start by defining the random variable ⇒
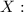 '' Number of students that will get 7 marks out of 10 in first attempt of a certain Quiz while attempting Quiz on BlackBoard LMS ''
'' Number of students that will get 7 marks out of 10 in first attempt of a certain Quiz while attempting Quiz on BlackBoard LMS ''
 is a discrete random variable.
is a discrete random variable.
The probability of a randomly selected student getting 7 marks out of 10 is 0.4
(This is a data from the question).
Now, if we assume independence between the students while they are doing the Quiz and also we assume that this probability remains constant , we can modelate
 as a binomial random variable ⇒
as a binomial random variable ⇒
 ~ Bi (n,p)
~ Bi (n,p)
Where ''n'' and ''p'' are the parameters of the variable.
''n'' is the number of students attempting the Quiz and ''p'' is the probability that a student will get 7 marks out of 10 which is 0.4 ⇒
 ~ Bi (20, 0.4) in the question.
~ Bi (20, 0.4) in the question.
The probability function for
 is
is
 (I)
(I)
Where
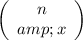 is the combinatorial number define as
is the combinatorial number define as
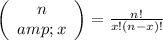
Replacing the parameters in the equation (I) ⇒
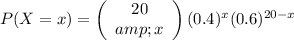 (II)
(II)
For i) we need to find
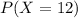
Then, we only need to replace by
 in equation (II) ⇒
in equation (II) ⇒
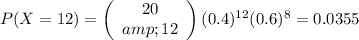
For ii) we need to calculate
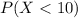
This probability is equal to ⇒
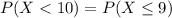 and to calculate it we need to sum
and to calculate it we need to sum
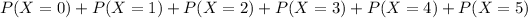
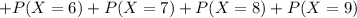
We can do it summing each term or either using any program.
The result is

Finally for iii) we need to find ⇒

This probability is equal to ⇒
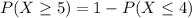 ⇒
⇒
![1-P(X\leq 4)=1-[P(X=0)+P(X=1)+P(X=2)+P(X=3)+P(X=4)]](https://img.qammunity.org/2021/formulas/mathematics/high-school/p0b4mbebvtxoynqesigaw0chkz02b70r77.png)
Again we can find each term by using the equation (II) or either using a program. The result is
