Question

In a container there are 2 liters of liquid, of which 75% is alcohol and the remaining 25% is water.

Determine how many cm3 of alcohol must be added to bring the alcohol percentage to 80%.

Answer 1

There must be added 500 cm3 of alcohol to bring the concentration to 80%.

Step-by-step explanation:

Concentration

The concentration of a solution is a measure of the amount of solute that has been dissolved in a given amount of solution.

In the container, there are 2 liters (2000 cubic centimeters) of a solution, 75% of which is alcohol (solute) and 25% of water (solvent).

The original amount of alcohol is:

H = 2000*75% = 1500 cc

The original amount of water is:

W = 2000*25% = 500 cc

When we add x cc of pure alcohol, there are 1500+x cc of alcohol out of 2000+x cc of solution.

The new concentration is calculated as:

`\displaystyle (1500+x)/(2000+x)`

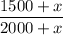
And it's known this concentration is 80% (0.8), thus:

`\displaystyle (1500+x)/(2000+x)=0.8`

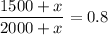
Multiplying by 2000+x:

`1500+x = 0.8(2000+x)`

Operating:

`1500+x = 1600+0.8x`

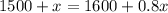
Rearranging:

`x-0.8x=1600-1500`

`0.2x=100`

`x=100/0.2`

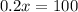
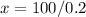
x= 500

There must be added 500 cm3 of alcohol to bring the concentration to 80%