Question

A baseball is thrown straight upward with a speed of 30 m/s. (a) How long will it rise? (6) How high will it

rise? (c) How long after it leaves the band will it return to the starting point? (ch) When will its speed be
16 m/s?

Answer 1

(a) 3.06 s

(b) 45.92 m

(c) 6.12 s

(ch) 1.43 s

Step-by-step explanation:

Vertical Launch Upwards

In a vertical launch upwards, an object is launched vertically up without taking into consideration any kind of friction with the air.

If vo is the initial speed and g is the acceleration of gravity, the maximum height reached by the object is given by:

`\displaystyle h_m=(v_o^2)/(2g)`

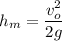
Similarly, the time it needs to reach the maximum height is:

`\displaystyle t_m=(v_o)/(g)`

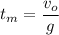
The object's speed (vf) after time t is:

`v_f=v_o-g.t`

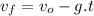
The baseball is thrown up at vo=30 m/s.

(a) It's required to calculate the time it needs to reach the maximum height:

`\displaystyle t_m=(30)/(9.8)=3.06`

`t_m=3.06~s`

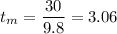
(b) The maximum height is:

`\displaystyle h_m=(30^2)/(2(9.8))=45.92`

`h_m=45.92~m`

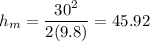
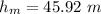
(c) The time needed to travel up is the same time required to return to the starting point:

`t_f=2*t_m=2*3.06`

`t_f=6.12~s`

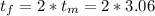
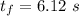
(ch) The speed will be vf=16 m/s at a certain time. Using the equation

`v_f=v_o-g.t`

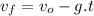
We solve for t:

`\displaystyle t=(v_f-v_o)/(g)`

`\displaystyle t=(30-16)/(9.8)`

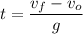
t = 1.43 s