Question

The first three terms of the binomial expansion of (2 – ax)" are 64 – 16bx +100bx?.

Find the value of each of the integers n, a and b.

Ans: n=6, a=5, b=60
​

Answer 1

n = 6, a = 5, b = 60

Explanation:

In a binomial function (a + b)ⁿ expression that represents the terms,

(a + b)ⁿ =
`\sum_(k=0)^(n)\binom{n}{k}a^(n-k)b^k`

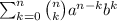
By this formula,

1st term =
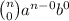`\binom{n}{0}a^(n-0)b^0` = aⁿ

2nd term =
`\binom{n}{1}a^(n-1)b^1` =
`n.a^(n-1)b^1`

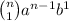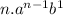
3rd term =
`\binom{n}{2}a^(n-2)b^2` =
`(n(n-1))/(2).a^(n-2).b^2`

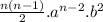
For the binomial expansion initial 3 terms of (2 - ax)ⁿ = 64 - 16bx + 100bx²

Terms of (2 - ax)ⁿ =
`2^n+n(2)^(n-1)(-ax)+(n(n-1))/(2)(2)^(n-2)(-ax)^2`

=
`2^n-n(2)^(n-1)(ax)+n(n-1)(2)^(n-3)(a^2x^2)`

Comparing the terms of both the expansions,

1st term

2ⁿ = 64

2ⁿ = 2⁶

n = 6

2d term

`n(2)^(n-1)(ax)=16bx`

`6(2)^(6-1)(a)=16b`

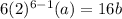
192a = 16b

b = 12a -----(1)

3rd term

`n(n-1)2^(n-3)(a^2x^2)=100bx^2`

`6(6-1)2^((6-3))(a^2)=100b`

`30(2)^3(a^2)=100b`

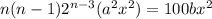
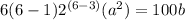
240a² = 100b

b = 2.4a² -----(2)

From equation (1) and (2),

b = 12a = 2.4a²

a =
`(12)/(2.4)=5`

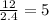
From equation (1)

b = 12a = 60

Therefore, n = 6, a = 5, b = 60