Question

Just look at the picture lol.....The equations of three lines are given below. Line 1: 8x-6y=-2 3 Line 2: y=-x-5 4 Line 3: 4y=-3x+3 For each pair of lines, determine whether they are parallel, perpendicular, or neither. Line 1 and Line 2: Parallel O Perpendicular O Neither Х Line 1 and Line 3: O Parallel O Perpendicular O Neither Line 2 and Line 3: Parallel O Perpendicular Neither​

Answer 1

Explanation:

We will use the following steps to solve this problem,

Step - (1).

Covert the equations into slope-intercept form.

Step - (2)

If the slopes of the two lines are equal, lines will be parallel.

`m_1=m_2`

Step - (3)

If the slopes of the two lines are negative reciprocal, lines will be perpendicular.

`m_1* m_2=-1`

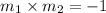
Line 1: 8x - 6y = -2

6y = 8x +2

y =
`(4)/(3)x+(1)/(3)`

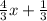
Slope of line 1 =
`m_1=(4)/(3)`

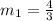
Line 2: y =
`-(3)/(4)x-5`

Slope of line 2 =
`m_2=-(3)/(4)`

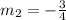
Line 3: 4y = -3x + 3

y =
`-(3)/(4)x+(3)/(4)`

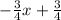
Slope of line 3 =
`m_3=-(3)/(4)`

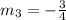
1). Since,
`m_1* m_2=(4)/(3)* (-(3)/(4))=-1`

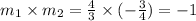
Line 1 and line 2 are perpendicular.

2). Since,
`m_1* m_3=(4)/(3)* (-(3)/(4))=-1`

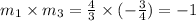
Line 1 and line 2 are perpendicular.

3). Since,
`m_2=m_3=-(3)/(4)`

Line 2 and line 3 are parallel.