Answer:
![\frac{x^(3)\sqrt[3]{x} }{4}](https://img.qammunity.org/2021/formulas/mathematics/college/yozgayqyqsils3jp4ka1392trb02qw3z1z.png)
Explanation:
*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^
What this is saying is it is taking the cubed root (which is like a square root, except it is using a 3 instead of 2) of x to the power of 10 divided by 64.
The equation is also saying:
![\frac{\sqrt[3]{x^(10) }}{\sqrt[3]{64} }](https://img.qammunity.org/2021/formulas/mathematics/college/se4d4zucqtp7qnib8wnjqztyp67dftt7ak.png)
We can simplify the bottom half of the fraction to be 4. The cube root of something is essentially saying its the number times itself 3 times (in this case, divided by that original number). The number to get to 64 was 4 and it was done like this: 4 times 4 times 4 (which equals 64).
As for the top equation, it will simplify down to
![x^(3) \sqrt[3]{x}](https://img.qammunity.org/2021/formulas/mathematics/college/zi4o8jjc07at4kyyrzhxm36k6sjss67qcl.png) .
.
Since
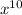 can be broken up to be x and
can be broken up to be x and
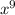 , we cube root the
, we cube root the
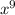 to become
to become
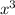 , while the x remains the same.
, while the x remains the same.
We come to result of
![\frac{x^(3)\sqrt[3]{x} }{4}](https://img.qammunity.org/2021/formulas/mathematics/college/yozgayqyqsils3jp4ka1392trb02qw3z1z.png) , which is the answer.
, which is the answer.
*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^*^
#teamtrees #WAP (Water And Plant)