Question

What are the equations of the asymptotes of the hyperbola?


`((y+4)^(2) )/(36)` -
`((x-6)^(2) )/(49)` =1


Enter your answer in point-slope form by filling in the boxes. Enter the slope as a simplified fraction.

Answer 1

hyperbola?

`((y+4)^(2) )/(36)` -
`((x-6)^(2) )/(49)` =1

Enter your answer in point-slope form by filling in the boxes. Enter the slope as a simplified fraction.

Answer 2

The equations of the asymptotes of the hyperbola in point-slope form are y + 4 = ±6/7(x - 6).

In Mathematics, the standard form of the equation of a vertical hyperbola is represented by this mathematical equation:

`((y\;-\;k)^2)/(a^2) - ((x\;-\;h)^2)/(b^2) =1`

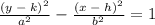
Where:

• a represents the semi-major axis.
• b represents the semi-minor axis.
• h and k represents the center.
• y and x represents the point.

Based on the information provided, we have the following equation of a hyperbola:

`((y\;+\;4)^2)/(36)-((x\;-\;6)^2)/(49) =1`

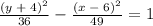
By rewriting the equation above in standard form, we have:

`((y\;+\;4)^2)/(6^2)-((x\;-\;6)^2)/(7^2) =1`

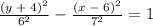
By comparing the new equation with the standard form, we can logically deduce the following parameters;

k = -4

a = 6

h = 6

b = 7

Furthermore, the standard form of the equation of the asymptote of a hyperbola is given by;

y = ±a/b(x - h) + k

y = ±6/7(x - 6) + (-4)

y = ±6/7(x - 6) - 4

By rewriting the equation above in point-slope form, we have:

y + 4 = ±6/7(x - 6)