1 Answer

Ask a Question

Gjorgji Tashkovski · Answer 1 · 2021-09-11T02:24:46+0000

Diagram:-

Required Answer:-

Tools Needed:

pencil, paper, ruler

Draw:-
$\begin{align*}\triangle ABC\end{align*}.$ Label the vertices.

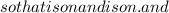$\begin{align*}\overline{XY}\end{align*} so that \begin{align*}X\end{align*} is on \begin{align*}\overline{AB}\end{align*} and \begin{align*}Y\end{align*} is on \begin{align*}\overline{BC}\end{align*}. \begin{align*}X\end{align*} and \begin{align*}Y\end{align*}$ can be anywhere on these sides.

Is
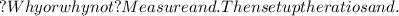$\begin{align*}\triangle XBY \sim \triangle ABC\end{align*}? Why or why not? Measure \begin{align*}AX, XB, BY,\end{align*} and \begin{align*}YC\end{align*}. Then set up the ratios \begin{align*}(AX)/(XB)\end{align*} and \begin{align*}(YC)/(YB)\end{align*}.$ Are they equal?

Draw:-

a second triangle,
$\begin{align*}\triangle DEF\end{align*}.$ Label the vertices

Draw:-

$\begin{align*}\overline{XY}\end{align*} so that \begin{align*}X\end{align*} is on \begin{align*}\overline{DE}\end{align*} and \begin{align*}Y\end{align*} is on \begin{align*}\overline{EF}\end{align*} AND \begin{align*}\overline{XY} \ || \ \overline{DF}\end{align*}.</p><p>Is \begin{align*}\triangle XEY \sim \triangle DEF\end{align*}? Why or why not? Measure \begin{align*}DX, XE, EY,\end{align*} and \begin{align*}YF\end{align*}. Then set up the ratios \begin{align*}(DX)/(XE)\end{align*} and \begin{align*}(FY)/(YE)\end{align*}.$ Are they equal?

From this investigation, it is clear that if the line segments are parallel, then
$\begin{align*}\overline{XY}\end{align*}$ divides the sides proportionally.

Plesase solve this Prove that a line parallel to one side of a triangle divides the-example-1

Plesase solve this Prove that a line parallel to one side of a triangle divides the-example-2

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.